For more than a month now Oliver and I have been walking to Birchwood Intermediate School every morning just past 8 o’clock. The old walk up Prince Street to Prince Street Elementary was simple: we walked up Prince Street. Birchwood is northeast of our house, though, and so there are a seemingly infinite ways of getting there.
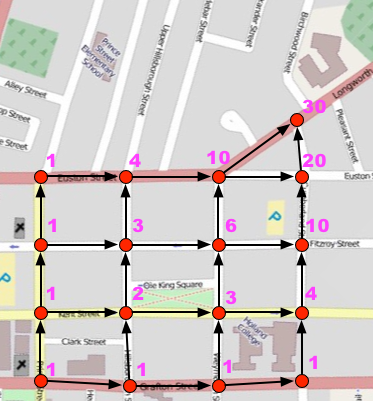
Actually, it turns out that there are 30 ways.
I figured this out using something called Pascal’s triangle. Here’s a simplified version of the street grid that covers the ground between the corner of Prince and Grafton (home) and the corner of Birchwood and Longworth (school) overlaid with the Pascal’s triangle’s binomial coefficients.
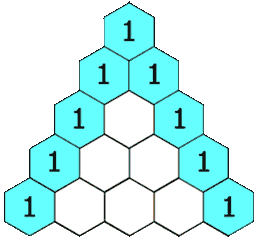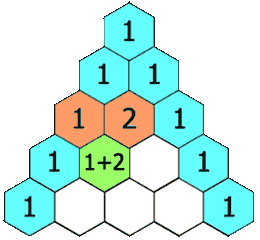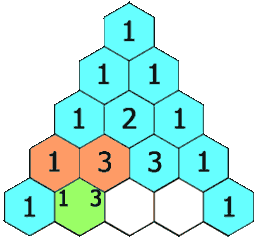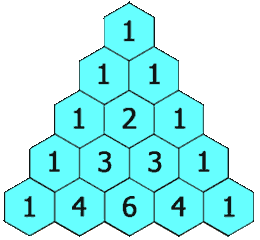
It took me a while to get my atrophied brain to understand Pascal’s triangle: this tutorial helped as did this animated GIF from Wikipedia:
This explanation sums it up well:
The first and last entry in each row of Pascal’s triangle is a 1. Every other entry in Pascal’s triangle is the sum of the two entries in the preceding row that lie to the immediate left and right.
So, in other words, we could go Prince-Kent-Hillsborough-Fitzroy-Weymouth-Longworth, or we could go Prince-Euston-Longworth, or we could go Grafton-Cumberland, or we could go Grafton-Hillsborough-Euston-Longworth. Total up the number of possible routes and the total is 30.
If we happened to take any of the 10 routes that pass through the corner of Longworth and Euston, we pass by a Maritime Electric pole in front of 27 Longworth that, for the first few weeks we walked by, looked like this:

I’m a tall guy and that guy wire, often hard to see in the morning sun, was positioned at the right height to catch my head if walking 2-by-2 with Oliver.
But problems have solutions, we tell Oliver.
And so I wrote a quick email to Kim Griffin, personable and award-winning “Manager, Corporate Communications & Public Affairs” at Maritime Electric. She was quick to reply – on a Sunday, no less – and by Monday morning the guy wire had been tightened up and shrouded in a protective and easy-to-see yellow shroud.
Many lessons learned.
 I am
I am
Comments
You might enjoy this math
You might enjoy this math puzzle tv series about using math to solve (somewhat contrived)everday puzzles. This episode looks at Pascal’s Triangle, probability and the Bell Curve. http://youtu.be/uan7tZImcFA
I used to draw diagrams like
I used to draw diagrams like and think about the same probabilities when I was modeling enzyme activation. What you’ve drawn is very nearly like a three-subunit enzyme, in which each subunit undergoes through three sequential twists to assume the shape it needs to be in before all three subunits do something in unison (or b/c you can get to the end of your route by either of two final hops, the subunits’ final act in unison can happen even if one of the subunits had undergone only two out of three twists). The the equivalency of intermediate states (e.g. there are 4 equivalent states of the enzyme in which just one subunit has undergone only two out of the three twists) means there’s a lot of entropy in being only partway activated, relative to the amount in being either fully activated or fully inactivated. All else equal, that entropy bonus biases the activation equilibrium toward intermediate inactivation, so there needs to be an energetic payoff to twisting and the final concerted step for the enzyme to be fully activated (say if each twist was brought about by oxygen binding, like in hemoglobin). I had to say because this is one of the few things in the world I supposedly really know about.
Not “very nearly” but exactly
Not “very nearly” but exactly like the enzyme situation. I wrote “very nearly” before I decided to account for there being two ways of making the final hop.
No, my bad. That’s not right.
No, my bad. That’s not right. What I described wouldn’t be square, but one triangular half of a square. Ugh. It was so long ago…
Ditto
Ditto
OK: On reflection, I think my
OK: On reflection, I think my mistake was to say the twists had to be completed sequentially. Your diagram is more like each of the three subunits has three levers, which can be thrown in any sequence.
Add new comment